Introduction and geometric constructions
Engineering drawing

An engineering drawing, a type of technical drawing, is used to fully and clearly define requirements for engineered items.
Engineering drawing (the activity) produces engineering drawings (the documents). More than merely the drawing of pictures, it is also a language—a graphical language that communicates ideas and information from one mind to another.[1] Most especially, it communicates all needed information from the engineer who designed a part to the workers who will make it.
Overview
Relationship to artistic drawing
Engineering drawing and artistic drawing are both types of drawing, and either may be called simply "drawing" when the context is implicit. Engineering drawing shares some traits with artistic drawing in that both create pictures. But whereas the purpose of artistic drawing is to convey emotion or artistic sensitivity in some way (subjective impressions), the purpose of engineering drawing is to convey information (objective facts). One of the corollaries that follows from this fact is that, whereas anyone can appreciate artistic drawing (even if each viewer has his own unique appreciation), engineering drawing requires some training to understand (like any language); but there is also a high degree of objective commonality in the interpretation (also like other languages). In fact, engineering drawing has evolved into a language that is more precise and unambiguous thannatural languages; in this sense it is closer to a programming language in its communication ability. Engineering drawing uses an extensive set of conventions to convey information very precisely, with very little ambiguity.
Relationship to other technical drawing types
The process of producing engineering drawings, and the skill of producing those, is often referred to as technical drawing or drafting (also spelled draughting), although technical drawings are also required for disciplines that would not ordinarily be thought of as parts of engineering (such as architecture, landscaping, cabinet making, and garment-making).
Persons employed in the trade of producing engineering drawings were called Draftsmen, or Draughtsmen in the past . Though these terms are still in use, recently they have been supplanted by gender neutral terms like draftsperson, or more commonly, drafter.
Cascading of conventions by specialty
The various fields share many common conventions of drawing, while also having some field-specific conventions. For example, even within metalworking, there are some process-specific conventions to be learned—casting, machining, fabricating, and assembly all have some special drawing conventions, and within fabrication there is further division, including welding, riveting, pipefitting, and erecting. Each of these trades has some details that only specialists will have memorized.
Legal instruments
An engineering drawing is a legal document (that is, a legal instrument), because it communicates all the needed information about "what is wanted" to the people who will expend resources turning the idea into a reality. It is thus a part of a contract; the purchase order and the drawing together, as well as any ancillary documents (engineering change orders [ECOs], called-out specs), constitute the contract. Thus, if the resulting product is wrong, the worker or manufacturer are protected from liability as long as they have faithfully executed the instructions conveyed by the drawing. If those instructions were wrong, it is the fault of the engineer. Because manufacturing and construction are typically very expensive processes (involving large amounts of capital and payroll), the question of liability for errors has great legal implications as each party tries to blame the other and assign the wasted cost to the other's responsibility. This is the biggest reason why the conventions of engineering drawing have evolved over the decades toward a very precise, unambiguous state.
Standardization and disambiguation
Engineering drawings specify requirements of a component or assembly which can be complicated. Standards provide rules for their specification and interpretation. In 2011, a new revision of ISO 8015 was published containing the Invocation Principle. This states that, "Once a portion of the ISO GPS system is invoked in a mechanical engineering product documentation, the entire ISO GPS system is invoked." It also goes on to state that marking a drawing "Tolerancing ISO 8015" is optional. The implication of this is that any drawing using ISO symbols can only be interpreted to ISO GPS rules. The only way not to invoke the ISO GPS system is to invoke a national or other standard.
Since there are only two widely standardized definitions of size, there is only one real alternative to ISO GPS, i.e. ASME Y14.5 and Y14.5M (most recently revised in 2009). Standardization also aids internationalization, because people from different countries who speak different languages can read the same engineering drawing, and interpret it the same way. To that end, drawings should be as free of notes and abbreviations as possible so that the meaning is conveyed graphically.
Media
For centuries, until the post-World War II era, all engineering drawing was done manually by using pencil and pen on paper or other substrate (e.g., vellum, mylar). Since the advent of computer-aided design (CAD), engineering drawing has been done more and more in the electronic medium with each passing decade. Today most engineering drawing is done with CAD, but pencil and paper have not disappeared.
Some of the tools of manual drafting include pencils, pens and their ink, straightedges, T-squares, French curves, triangles, rulers, protractors, dividers, compasses, scales, erasers, and tacks or push pins. (Slide rules used to number among the supplies, too, but nowadays even manual drafting, when it occurs, benefits from a pocket calculator or its onscreen equivalent.) And of course the tools also include drawing boards (drafting boards) or tables. The English idiom "to go back to the drawing board", which is a figurative phrase meaning to rethink something altogether, was inspired by the literal act of discovering design errors during production and returning to a drawing board to revise the engineering drawing. Drafting machines are devices that aid manual drafting by combining drawing boards, straightedges, pantographs, and other tools into one integrated drawing environment. CAD provides their virtual equivalents.
Producing drawings usually involves creating an original that is then reproduced, generating multiple copies to be distributed to the shop floor, vendors, company archives, and so on. The classic reproduction methods involved blue and white appearances (whether white-on-blue or blue-on-white), which is why engineering drawings were long called, and even today are still often called, "blueprints" or "bluelines", even though those terms are anachronistic from a literal perspective, since most copies of engineering drawings today are made by more modern methods (often inkjet or laser printing) that yield black or multicolour lines on white paper. The more generic term "print" is now in common usage in the U.S. to mean any paper copy of an engineering drawing. In the case of CAD drawings, the original is the CAD file, and the printouts of that file are the "prints".
Relationship to model-based definition (MBD/DPD)
For centuries, engineering drawing was the sole method of transferring information from design into manufacture. In recent decades another method has arisen, called model-based definition (MBD) or digital product definition (DPD). In MBD, the information captured by the CAD software app is fed automatically into a CAM app (computer-aided manufacturing), and is translated via postprocessor into other languages such as G-code, which is executed by a CNC machine tool (computer numerical control). Thus today it is often the case that the information travels from the mind of the designer into the manufactured component without having ever been codified by an engineering drawing. In MBD, the dataset, not a drawing, is the legal instrument. The term "technical data package" (TDP) is now used to refer to the complete package of information (in one medium or another) that communicates information from design to production (such as 3D-model datasets, engineering drawings, engineering change orders (ECOs), spec revisions and addenda, and so on). However, even in the MBD era, where theoretically production could happen without any drawings or humans at all, it is still the case that drawings and humans are involved. It still takes CAD/CAM programmers, CNC setup workers, and CNC operators to do manufacturing, as well as other people such as quality assurance staff (inspectors) and logistics staff (for materials handling, shipping-and-receiving, and front office functions). These workers often use drawings in the course of their work that have been produced by rendering and plotting (printing) from the MBD dataset. When proper procedures are being followed, a clear chain of precedence is always documented, such that when a person looks at a drawing, s/he is told by a note thereon that this drawing is not the governing instrument (because the MBD dataset is). In these cases, the drawing is still a useful document, although legally it is classified as "for reference only", meaning that if any controversies or discrepancies arise, it is the MBD dataset, not the drawing, that governs.
Systems of dimensioning and tolerancing
Almost all engineering drawings (except perhaps reference-only views or initial sketches) communicate not only geometry (shape and location) but also dimensions andtolerances for those characteristics. Several systems of dimensioning and tolerancing have evolved. The simplest dimensioning system just specifies distances between points (such as an object's length or width, or hole center locations). Since the advent of well-developed interchangeable manufacture, these distances have been accompanied by tolerances of the plus-or-minus or min-and-max-limit types. Coordinate dimensioning involves defining all points, lines, planes, and profiles in terms of Cartesian coordinates, with a common origin. Coordinate dimensioning was the sole best option until the post-World War II era saw the development of geometric dimensioning and tolerancing (GD&T), which departs from the limitations of coordinate dimensioning (e.g., rectangular-only tolerance zones, tolerance stacking) to allow the most logical tolerancing of both geometry and dimensions (that is, both form [shapes/locations] and sizes).
Engineering drawings: common features
Drawings convey the following critical information:
- Geometry – the shape of the object; represented as views; how the object will look when it is viewed from various angles, such as front, top, side, etc.
- Dimensions – the size of the object is captured in accepted units.
- Tolerances – the allowable variations for each dimension.
- Material – represents what the item is made of.
- Finish – specifies the surface quality of the item, functional or cosmetic. For example, a mass-marketed product usually requires a much higher surface quality than, say, a component that goes inside industrial machinery.
Line styles and types[edit]

A variety of line styles graphically represent physical objects. Types of lines include the following:
- visible – are continuous lines used to depict edges directly visible from a particular angle.
- hidden – are short-dashed lines that may be used to represent edges that are not directly visible.
- center – are alternately long- and short-dashed lines that may be used to represent the axes of circular features.
- cutting plane – are thin, medium-dashed lines, or thick alternately long- and double short-dashed that may be used to define sections forsection views.
- section – are thin lines in a pattern (pattern determined by the material being "cut" or "sectioned") used to indicate surfaces in section views resulting from "cutting." Section lines are commonly referred to as "cross-hatching."
- phantom - (not shown) are alternately long- and double short-dashed thin lines used to represent a feature or component that is not part of the specified part or assembly. E.g. billet ends that may be used for testing, or the machined product that is the focus of a tooling drawing.
Lines can also be classified by a letter classification in which each line is given a letter.
- Type A lines show the outline of the feature of an object. They are the thickest lines on a drawing and done with a pencil softer than HB.
- Type B lines are dimension lines and are used for dimensioning, projecting, extending, or leaders. A harder pencil should be used, such as a 2H.
- Type C lines are used for breaks when the whole object is not shown. These are freehand drawn and only for short breaks. 2H pencil
- Type D lines are similar to Type C, except these are zigzagged and only for longer breaks. 2H pencil
- Type E lines indicate hidden outlines of internal features of an object. These are dotted lines. 2H pencil
- Type F lines are Type F[typo] lines, except these are used for drawings in electrotechnology. 2H pencil
- Type G lines are used for centre lines. These are dotted lines, but a long line of 10–20 mm, then a gap, then a small line of 2 mm. 2H pencil
- Type H lines are the same as Type G, except that every second long line is thicker. These indicate the cutting plane of an object. 2H pencil
- Type K lines indicate the alternate positions of an object and the line taken by that object. These are drawn with a long line of 10–20 mm, then a small gap, then a small line of 2 mm, then a gap, then another small line. 2H pencil.
Multiple views and projections
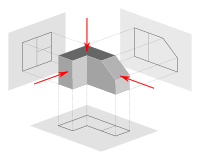
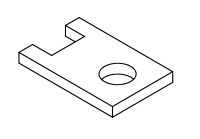
In most cases, a single view is not sufficient to show all necessary features, and several views are used. Types of views include the following:
Orthographic projection
The orthographic projection shows the object as it looks from the front, right, left, top, bottom, or back, and are typically positioned relative to each other according to the rules of either first-angle or third-angle projection. The origin and vector direction of the projectors (also called projection lines) differs, as explained below.
- In first-angle projection, the projectors originate as if radiated from a viewer's eyeballs and shoot through the 3D object to project a 2D image onto the plane behind it. The 3D object is projected into 2D "paper" space as if you were looking at a radiograph of the object: the top view is under the front view, the right view is at the left of the front view. First-angle projection is the ISO standard and is primarily used in Europe.
- In third-angle projection, the projectors originate as if radiated from the 3D object itself and shoot away from the 3D object to project a 2D image onto the plane in front of it. The views of the 3D object are like the panels of a box that envelopes the object, and the panels pivot as they open up flat into the plane of the drawing. Thus the left view is placed on the left and the top view on the top; and the features closest to the front of the 3D object will appear closest to the front view in the drawing. Third-angle projection is primarily used in the United States and Canada, where it is the default projection system according to ASME standard ASME Y14.3M.
Until the late 19th century, first-angle projection was the norm in North America as well as Europe; but circa the 1890s, the meme of third-angle projection spread throughout the North American engineering and manufacturing communities to the point of becoming a widely followed convention, and it was an ASA standard by the 1950s. Circa World War I, British practice was frequently mixing the use of both projection methods.
As shown above, the determination of what surface constitutes the front, back, top, and bottom varies depending on the projection method used.
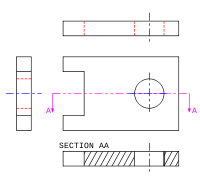
Not all views are necessarily used. Generally only as many views are used as are necessary to convey all needed information clearly and economically.The front, top, and right-side views are commonly considered the core group of views included by default, but any combination of views may be used depending on the needs of the particular design. In addition to the 6 principal views (front, back, top, bottom, right side, left side), any auxiliary views or sections may be included as serve the purposes of part definition and its communication. View lines or section lines (lines with arrows marked "A-A", "B-B", etc.) define the direction and location of viewing or sectioning. Sometimes a note tells the reader in which zone(s) of the drawing to find the view or section.
Auxiliary projection
An auxiliary view is an orthographic view that is projected into any plane other than one of the six principal views. These views are typically used when an object contains some sort of inclined plane. Using the auxiliary view allows for that inclined plane (and any other significant features) to be projected in their true size and shape. The true size and shape of any feature in an engineering drawing can only be known when the Line of Sight (LOS) is perpendicular to the plane being referenced. It is shown like a three-dimensional object.
Isometric projection
The isometric projection show the object from angles in which the scales along each axis of the object are equal. Isometric projection corresponds to rotation of the object by ± 45° about the vertical axis, followed by rotation of approximately ± 35.264° [= arcsin(tan(30°))] about the horizontal axis starting from an orthographic projection view. "Isometric" comes from the Greek for "same measure". One of the things that makes isometric drawings so attractive is the ease with which 60 degree angles can be constructed with only acompass and straightedge.
Isometric projection is a type of axonometric projection. The other two types of axonometric projection are:
- Dimetric projection
- Trimetric projection
Oblique projection
An oblique projection is a simple type of graphical projection used for producing pictorial, two-dimensional images of three-dimensional objects:
- it projects an image by intersecting parallel rays (projectors)
- from the three-dimensional source object with the drawing surface (projection plan).
In both oblique projection and orthographic projection, parallel lines of the source object produce parallel lines in the projected image.
Perspective
Perspective is an approximate representation on a flat surface, of an image as it is perceived by the eye. The two most characteristic features of perspective are that objects are drawn:
- Smaller as their distance from the observer increases
- Foreshortened: the size of an object's dimensions along the line of sight are relatively shorter than dimensions across the line of sight.
Section Views
Projected views (either Auxiliary or Orthographic) which show a cross section of the source object along the specified cut plane. These views are commonly used to show internal features with more clarity than may be available using regular projections or hidden lines. In assembly drawings, hardware components (e.g. nuts, screws, washers) are typically not sectioned.
Scale
Plans are usually "scale drawings", meaning that the plans are drawn at specific ratio relative to the actual size of the place or object. Various scales may be used for different drawings in a set. For example, a floor plan may be drawn at 1:50 (1:48 or 1/4"=1'-0") whereas a detailed view may be drawn at 1:25 (1:24 or 1/2"=1'-0"). Site plans are often drawn at 1:200 or 1:100.
Scale is a nuanced subject in the use of engineering drawings. On one hand, it is a general principle of engineering drawings that they are projected using standardized, mathematically certain projection methods and rules. Thus, great effort is put into having an engineering drawing accurately depict size, shape, form, aspect ratios between features, and so on. And yet, on the other hand, there is another general principle of engineering drawing that nearly diametrically opposes all this effort and intent—that is, the principle that users are not to scale the drawing to infer a dimension not labeled. This stern admonition is often repeated on drawings, via a boilerplate note in the title block telling the user, "DO NOT SCALE DRAWING."
The explanation for why these two nearly opposite principles can coexist is as follows. The first principle—that drawings will be made so carefully and accurately—serves the prime goal of why engineering drawing even exists, which is successfully communicating part definition and acceptance criteria—including "what the part should look like if you've made it correctly." The service of this goal is what creates a drawing that one even could scale and get an accurate dimension thereby. And thus the great temptation to do so, when a dimension is wanted but was not labeled. The second principle—that even though scaling the drawing will usually work, one should nevertheless never do it—serves several goals, such as enforcing total clarity regarding who has authority to discern design intent, and preventing erroneous scaling of a drawing that was never drawn to scale to begin with (which is typically labeled "drawing not to scale" or "scale: NTS"). When a user is forbidden from scaling the drawing, s/he must turn instead to the engineer (for the answers that the scaling would seek), and s/he will never erroneously scale something that is inherently unable to be accurately scaled.
But in some ways, the advent of the CAD and MBD era challenges these assumptions that were formed many decades ago. When part definition is defined mathematically via a solid model, the assertion that one cannot interrogate the model—the direct analog of "scaling the drawing"—becomes ridiculous; because when part definition is defined this way, it is not possible for a drawing or model to be "not to scale". A 2D pencil drawing can be inaccurately foreshortened and skewed (and thus not to scale), yet still be a completely valid part definition as long as the labeled dimensions are the only dimensions used, and no scaling of the drawing by the user occurs. This is because what the drawing and labels convey is in reality a symbol of what is wanted, rather than a true replica of it. (For example, a sketch of a hole that is clearly not round still accurately defines the part as having a true round hole, as long as the label says "10mm DIA", because the "DIA" implicitly but objectively tells the user that the skewed drawn circle is a symbolrepresenting a perfect circle.) But if a mathematical model—essentially, a vector graphic—is declared to be the official definition of the part, then any amount of "scaling the drawing" can make sense; there may still be an error in the model, in the sense that what was intended is not depicted (modeled); but there can be no error of the "not to scale" type—because the mathematical vectors and curves are replicas, not symbols, of the part features.
Even in dealing with 2D drawings, the manufacturing world has changed since the days when people paid attention to the scale ratio claimed on the print, or counted on its accuracy. In the past, prints were plotted on a plotter to exact scale ratios, and the user could know that a line on the drawing 15mm long corresponded to a 30mm part dimension because the drawing said "1:2" in the "scale" box of the title block. Today, in the era of ubiquitous desktop printing, where original drawings or scaled prints are often scanned on a scanner and saved as a PDF file, which is then printed at any percent magnification that the user deems handy (such as "fit to paper size"), users have pretty much given up caring what scale ratio is claimed in the "scale" box of the title block. Which, under the rule of "do not scale drawing", never really did that much for them anyway.
Showing dimensions
The required sizes of features are conveyed through use of dimensions. Distances may be indicated with either of two standardized forms of dimension: linear and ordinate.
- With linear dimensions, two parallel lines, called "extension lines," spaced at the distance between two features, are shown at each of the features. A line perpendicular to the extension lines, called a "dimension line," with arrows at its endpoints, is shown between, and terminating at, the extension lines. The distance is indicated numerically at the midpoint of the dimension line, either adjacent to it, or in a gap provided for it.
- With ordinate dimensions, one horizontal and one vertical extension line establish an origin for the entire view. The origin is identified with zeroes placed at the ends of these extension lines. Distances along the x- and y-axes to other features are specified using other extension lines, with the distances indicated numerically at their ends.
Sizes of circular features are indicated using either diametral or radial dimensions. Radial dimensions use an "R" followed by the value for the radius; Diametral dimensions use a circle with forward-leaning diagonal line through it, called the diameter symbol, followed by the value for the diameter. A radially-aligned line with arrowhead pointing to the circular feature, called a leader, is used in conjunction with both diametral and radial dimensions. All types of dimensions are typically composed of two parts: the nominal value, which is the "ideal" size of the feature, and the tolerance, which specifies the amount that the value may vary above and below the nominal.
- Geometric dimensioning and tolerancing is a method of specifying the functional geometry of an object.
Sizes of drawings
Sizes of drawings typically comply with either of two different standards, ISO (World Standard) or ANSI/ASME Y14 (American), according to the following tables:
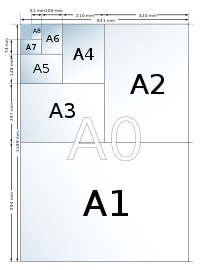
| A4 | 210 X 297 |
|---|---|
| A3 | 297 X 420 |
| A2 | 420 X 594 |
| A1 | 594 X 841 |
| A0 | 841 X 1189 |
| A | 8.5" X 11" |
|---|---|
| B | 11" X 17" |
| C | 17" X 22" |
| D | 22" X 34" |
| E | 34" X 44" |
| D1 | 24" X 36" |
|---|---|
| E1 | 30" X 42" |
| H | larger still [intracompany standards] |
| I | larger still [intracompany standards] |
| J | larger still [intracompany standards] |
The metric drawing sizes correspond to international paper sizes. These developed further refinements in the second half of the twentieth century, when photocopying became cheap. Engineering drawings could be readily doubled (or halved) in size and put on the next larger (or, respectively, smaller) size of paper with no waste of space. And the metric technical pens were chosen in sizes so that one could add detail or drafting changes with a pen width changing by approximately a factor of the square root of 2. A full set of pens would have the following nib sizes: 0.13, 0.18, 0.25, 0.35, 0.5, 0.7, 1.0, 1.5, and 2.0 mm. However, the International Organization for Standardization (ISO) called for four pen widths and set a colour code for each: 0.25 (white), 0.35 (yellow), 0.5 (brown), 0.7 (blue); these nibs produced lines that related to various text character heights and the ISO paper sizes.
All ISO paper sizes have the same aspect ratio, one to the square root of 2, meaning that a document designed for any given size can be enlarged or reduced to any other size and will fit perfectly. Given this ease of changing sizes, it is of course common to copy or print a given document on different sizes of paper, especially within a series, e.g. a drawing on A3 may be enlarged to A2 or reduced to A4.
The U.S. customary "A-size" corresponds to "letter" size, and "B-size" corresponds to "ledger" or "tabloid" size. There were also once British paper sizes, which went by names rather than alphanumeric designations.
American Society of Mechanical Engineers (ASME) Y14.2, Y14.3, and Y14.5 are commonly referenced standards in the U.S.
Technical lettering
Technical lettering is the process of forming letters, numerals, and other characters in technical drawing. It is used to describe, or provide detailed specifications for, an object. With the goals of legibility and uniformity, styles are standardized and lettering ability has little relationship to normal writing ability. Engineering drawings use a Gothic sans-serifscript, formed by a series of short strokes. Lower case letters are rare in most drawings of machines. ISO Lettering templates, designed for use with technical pens and pencils, and to suit ISO paper sizes, produce lettering characters to an international standard. The stroke thickness is related to the character height (for example, 2.5mm high characters would have a stroke thickness - pen nib size - of 0.25mm, 3.5 would use a 0.35mm pen and so forth). The ISO character set (font) has a seriffed one, a barred seven, an open four, six, and nine, and a round topped three, that improves legibility when, for example, an A0 drawing has been reduced to A1 or even A3 (and perhaps enlarged back or reproduced/faxed/ microfilmed &c). When CAD drawings became more popular, especially using US American software, such as AutoCAD, the nearest font to this ISO standard font was Romantic Simplex (RomanS) - a proprietary shx font) with a manually adjusted width factor (over ride) to make it look as near to the ISO lettering for the drawing board. However, with the closed four, and arced six and nine, romans.shx typeface could be difficult to read in reductions. In more recent revisions of software packages, the TrueTypefont ISOCPEUR reliably reproduces the original drawing board lettering stencil style, however, many drawings have switched to the ubiquitous Arial.ttf.
Conventional parts (areas) of an engineering drawing
Title block
The title block (T/B, TB) is an area of the drawing that conveys header-type information about the drawing, such as:
- Drawing title (hence the name "title block")
- Drawing number
- Part number(s)
- Name of the design activity (corporation, government agency, etc.)
- Identifying code of the design activity (such as a CAGE code)
- Address of the design activity (such as city, state/province, country)
- Measurement units of the drawing (for example, inches, millimeters)
- Default tolerances for dimension callouts where no tolerance is specified
- Boilerplate callouts of general specs
- Intellectual property rights warning
Traditional locations for the title block are the bottom right (most commonly) or the top right or center.
Revisions block
The revisions block (rev block) is a tabulated list of the revisions (versions) of the drawing, documenting the revision control.
Traditional locations for the revisions block are the top right (most commonly) or adjoining the title block in some way.
Next assembly
The next assembly block, often also referred to as "where used" or sometimes "effectivity block", is a list of higher assemblies where the product on the current drawing is used. This block is commonly found adjacent to the title block.
Notes list
The notes list provides notes to the user of the drawing, conveying any information that the callouts within the field of the drawing did not. It may include general notes, flagnotes, or a mixture of both.
Traditional locations for the notes list are anywhere along the edges of the field of the drawing.
General notes
General notes (G/N, GN) apply generally to the contents of the drawing, as opposed to applying only to certain part numbers or certain surfaces or features.
Flagnotes
Flagnotes or flag notes (FL, F/N) are notes that apply only where a flagged callout points, such as to particular surfaces, features, or part numbers. Typically the callout includes a flag icon. Some companies call such notes "delta notes", and the note number is enclosed inside a triangular symbol (similar to capital letter delta, Δ). "FL5" (flagnote 5) and "D5" (delta note 5) are typical ways to abbreviate in ASCII-only contexts.
Field of the drawing
The field of the drawing (F/D, FD) is the main body or main area of the drawing, excluding the title block, rev block, and so on.
List of materials, bill of materials, parts lis
The list of materials (L/M, LM, LoM), bill of materials (B/M, BM, BoM), or parts list (P/L, PL) is a (usually tabular) list of the materials used to make a part, and/or the parts used to make an assembly. It may contain instructions for heat treatment, finishing, and other processes, for each part number. Sometimes such LoMs or PLs are separate documents from the drawing itself.
Traditional locations for the LoM/BoM are above the title block, or in a separate document.
Parameter tabulations
Some drawings call out dimensions with parameter names (that is, variables, such a "A", "B", "C"), then tabulate rows of parameter values for each part number.
Traditional locations for parameter tables, when such tables are used, are floating near the edges of the field of the drawing, either near the title block or elsewhere along the edges of the field.
Views and sections
Each view or section is a separate set of projections, occupying a contiguous portion of the field of the drawing. Usually views and sections are called out with cross-references to specific zones of the field.
Zones
Often a drawing is divided into zones by a grid, with zone labels along the margins, such as A,B,C,D up the sides and 1,2,3,4,5,6 along the top and bottom. Names of zones are thus, for example, A5, D2, or B1. This feature greatly eases discussion of, and reference to, particular areas of the drawing.
Abbreviations and symbols
As in many technical fields, a wide array of abbreviations and symbols have been developed in engineering drawing during the 20th and 21st centuries. For example, cold rolled steel is often abbreviated as CRS, and diameter is often abbreviated as DIA, D, or ⌀.
Example of an engineering drawing
Here is an example of an engineering drawing (an isometric view of the same object is shown above). The different line types are colored for clarity.
- Black = object line and hatching
- Red = hidden line
- Blue = center line of piece or opening
- Magenta = phantom line or cutting plane line
Graphical projection
| Graphical projection |
|---|
 |
|
Planar[show]
|
|
Other[show]
|
|
Views[show]
|
|
Topics[show]
|
|
|

Graphical projection is a protocol by which an image of a three-dimensional object is projected onto a planar surface without the aid of numerical calculation, used in technical drawing.[
Overview

The projection is achieved by the use of imaginary "projectors". The projected, mental image becomes the technician’s vision of the desired, finished picture. By following the protocol the technician may produce the envisioned picture on a planar surface such as drawing paper. The protocols provide a uniform imaging procedure among people trained in technical graphics (mechanical drawing, computer aided design, etc.).
There are two graphical projection categories each with its own protocol:
- parallel projection
- perspective projection
-

Isometric projection.
-
Oblique projection.
-

Oblique projection.
-

One-point perspective projection.
Types of projection

Parallel projection
In parallel projection,the lines of sight from the object to the projection plane are parallel to each other. Within parallel projection there is an ancillary category known as "pictorials". Pictorials show an image of an object as viewed from a skew direction in order to reveal all three directions (axes) of space in one picture. Because pictorial projections innately contain this distortion, in the rote, drawing instrument for pictorials, some liberties may be taken for economy of effort and best effect.it is a simultaneous process of viewing the image give pictures
Orthographic projection
The Orthographic projection is derived from the principles of descriptive geometry and is a two-dimensional representation of a three-dimensional object. It is a parallel projection (the lines of projection are parallel both in reality and in the projection plane). It is the projection type of choice for working drawings.
Pictorials
Within parallel projection there is a subcategory known as Pictorials. Pictorials show an image of an object as viewed from a skew direction in order to reveal all three directions (axes) of space in one picture. Parallel projection pictorial instrument drawings are often used to approximate graphical perspective projections, but there is attendant distortion in the approximation. Because pictorial projections inherently have this distortion, in the instrument drawing of pictorials, great liberties may then be taken for economy of effort and best effect. Parallel projection pictorials rely on the technique of axonometric projection ("to measure along axes").
Axonometric projection
Axonometric projection is a type of parallel projection used to create a pictorial drawing of an object, where the object is rotated along one or more of its axes relative to the plane of projection.[1]
There are three main types of axonometric projection: isometric, dimetric, and trimetric projection.

Isometric projection
In isometric pictorials (for protocols see isometric projection), the direction of viewing is such that the three axes of space appear equally foreshortened, and there is a common angle of 60° between them. As the distortion caused by foreshortening is uniform the proportionality of all sides and lengths are preserved, and the axes share a common scale. This enables measurements to be read or taken directly from the drawing.
Dimetric projection
In dimetric pictorials (for protocols see dimetric projection), the direction of viewing is such that two of the three axes of space appear equally foreshortened, of which the attendant scale and angles of presentation are determined according to the angle of viewing; the scale of the third direction (vertical) is determined separately. Approximations are common in dimetric drawings.
Trimetric projection[edit]
In trimetric pictorials (for protocols see trimetric projection), the direction of viewing is such that all of the three axes of space appear unequally foreshortened. The scale along each of the three axes and the angles among them are determined separately as dictated by the angle of viewing. Approximations in Trimetric drawings are common.
Oblique projection
In oblique projections the parallel projection rays are not perpendicular to the viewing plane as with orthographic projection, but strike the projection plane at an angle other than ninety degrees. In both orthographic and oblique projection, parallel lines in space appear parallel on the projected image. Because of its simplicity, oblique projection is used exclusively for pictorial purposes rather than for formal, working drawings. In an oblique pictorial drawing, the displayed angles among the axes as well as the foreshortening factors (scale) are arbitrary. The distortion created thereby is usually attenuated by aligning one plane of the imaged object to be parallel with the plane of projection thereby creating a true shape, full-size image of the chosen plane. Special types of oblique projections are:
Cavalier projection
In cavalier projection (sometimes cavalier perspective or high view point) a point of the object is represented by three coordinates, x, y and z. On the drawing, it is represented by only two coordinates, x" and y". On the flat drawing, two axes, x and z on the figure, are perpendicular and the length on these axes are drawn with a 1:1 scale; it is thus similar to the dimetric projections, although it is not an orthographic projection, as the third axis, here y, is drawn in diagonal, making an arbitrary angle with the x" axis, usually 30 or 45°. The length of the third axis is not scaled.
Cabinet projection
The term cabinet projection (sometimes cabinet perspective) stems from its use in illustrations by the furniture industry.[citation needed] Like cavalier perspective, one face of the projected object is parallel to the viewing plane, and the third axis is projected as going off in an angle (typical 30° or 45° or arctan(2)=63.4°). Unlike cavalier projection, where the third axis keeps its length, with cabinet projection the length of the receding lines is cut in half.
Perspective projection


Perspective projection is a linear projection where three dimensional objects are projected on a picture plane. This has the effect that distant objects appear smaller than nearer objects.
It also means that lines which are parallel in nature (that is, meet at the point at infinity) appear to intersect in the projected image, for example if railways are pictured with perspective projection, they appear to converge towards a single point, called vanishing point. Photographic lenses and the human eye work in the same way, therefore perspective projection looks most realistic.[2] Perspective projection is usually categorized into one-point, two-point and three-point perspective, depending on the orientation of the projection plane towards the axes of the depicted object.[3]
Graphical projection methods rely on the duality between lines and points, whereby two straight lines determine a point while two points determine a straight line. The orthogonal projection of the eye point onto the picture plane is called the principal vanishing point (P.P. in the scheme on the left, from the Italian term punto principale, coined during the renaissance).[4]
Two relevant points of a line are:
- its intersection with the picture plane, and
- its vanishing point, found at the intersection between the parallel line from the eye point and the picture plane.
The principal vanishing point is the vanishing point of all horizontal lines perpendicular to the picture plane. The vanishing points of all horizontal lines lie on the horizon line, obviously. If, as is often the case, the picture plane is vertical, all vertical lines are drawn vertically, and have no finite vanishing point on the picture plane. Various graphical methods can be easily envisaged for projecting geometrical scenes. For example, lines traced from the eye point at 45° to the picture plane intersect the latter along a circle whose radius is the distance of the eye point from the plane, thus tracing that circle aids the construction of all the vanishing points of 45° lines; in particular, the intersection of that circle with the horizon line consists of two distance points. They are useful for drawing chessboard floors which, in turn, serve for locating the base of objects on the scene. In the perspective of a geometric solid on the right, after choosing the principal vanishing point —which determines the horizon line— the 45° vanishing point on the left side of the drawing completes the characterization of the (equally distant) point of view. Two lines are drawn from the orthogonal projection of each vertex, one at 45° and one at 90° to the picture plane. After intersecting the ground line, those lines go toward the distance point (for 45°) or the principal point (for 90°). Their new intersection locates the projection of the map. Natural heights are measured above the ground line and then projected in the same way until they meet the vertical from the map.



























































































